第一章:复变和复变函数
1.1 复数与复数运算
复数的定义:
有序实数对(x,y)遵从以下规则:
则有序实数对(x,y)定义了一个复数
,其中x称为z的实部,y称为z的虚部。 记作:
复数相等的条件:实部和虚部分别相等
特殊的复数:1,i,0
- 当y=0时,
为实数,如实数1 - 当x=0时,记
, ,称为纯虚数 - 故复数可以表示成
- 由复数的运算法则可知
- 复数都存在其相反数
- 当y=0时,
加法与乘法:
- 由定义可知
- 复数的运算也满足交换律,结合律和分配律
- 乘方和开方定义与实数类似
共轭复数与复数除法:
共轭复数:
与 互称共轭复数 共轭复数的性质:
,
利用共轭复数可以计算复数的除法:
1.2 复数的几何表示
复平面:
- 复平面:用一个二维平面,横轴为x(称为实轴),纵轴为y(称为虚轴)
- 因此,复数可以用复平面上的一个点表示
- 复数也可以用复平面上的矢量来表示。因此复数的加法转化成矢量的加法,满足三角形法则/平行四边形法则,复数的减法可以转化成矢量的减法。
因此衍生出复数的极坐标表示:
- 因此复数可以用
和 表示 - r称为模
称为辅角,由于三角函数的周期性,辅角不止一个,因此把位于 之间的辅角值称为辅角的主值
- 复数的乘法:
- 复数的除法:
由欧拉公式衍生出复数的指数表示:
复数可以表示成:
同理,r为复数的模,
为复数的辅角 其满足指数函数同样的性质,如乘法和除法
负球面:
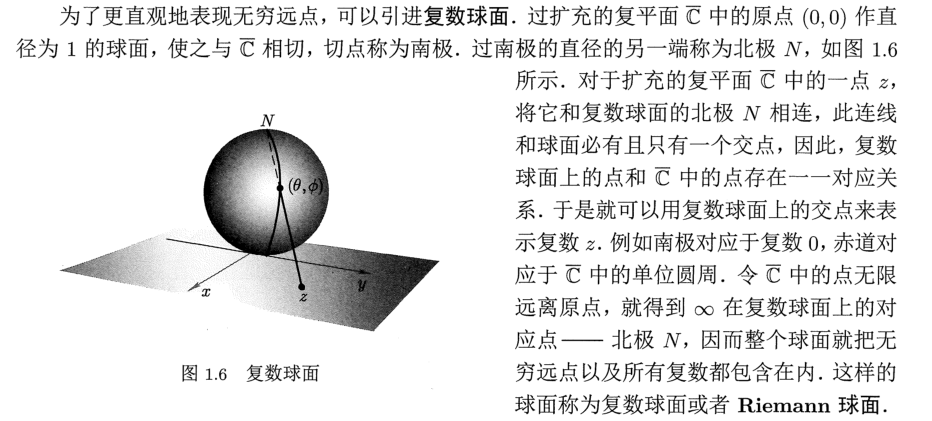
1.3 区域
- **区域的定义:**平面点集D作为一个区域
- D是一个开集
- D是连通的,即D中任何两点都可以用完全属于D的一条折线连接起来
- 边界:
- 边界点:P点不属于D,但是在P的任意小领域内总包含D中的点,则称P点为区域D的边界点
- D的所有边界点构成D的边界
- **闭区域:**区域D和它的边界构成闭区域,记作
- 单连通域和多连通域
- 单连通域:如果在区域内任意画一条闭合曲线(像一个圈),这条曲线都可以在不离开该区域的情况下,连续收缩成一个点
- 多连通域:如果区域内存在某些闭合曲线,无法在不离开区域的情况下收缩成一个点
1.4 复变函数
复变函数:
如果对于区域 G 内的每一个复数 z , 都有唯一一个复数 ω 与之对应, ω 和 z 之间的这种对应关系记为 f, 则称 f 为定义在 G 上的复变函数。
定义域:区域G称为函数f的定义域
复变函数相当于定义了两个二元实变函数:
- 给定
,对应的复数 - 相当于定义了两个二元实变函数
- 给定
通常,函数着重于说明复数与复数之间的对应关系.为了强调点与点之间的对应关系,我们也常把函数 ω = f(z) 称为映射(或变换) ,记为
其中 ω 称为 z 在映射 f 下的像 ,z称为 ω 的原像
给定一个自变量值,许可有多个函数值与之对应.这种对应关系,称为多值函数