1.1 数字信号与数字电路
- 电子电路分成组合逻辑电路和时序逻辑电路
- 模拟信号与数字信号
- 模拟信号:连续
- 数字信号:离散
- 模拟信号的数字表示:取样、量化、编码
- 数字信号的表述方法
- 二值数字逻辑和逻辑电平:
- 二值数字逻辑:用0和1表示的逻辑状态,可以进行运算
- 逻辑电平:使用H(高电平)和L(低电平)进行表示的逻辑关系。
- 数字波形:
- 类型:归零型和非归零型
- 周期性和非周期性
- 周期T
- 脉冲宽度
- 占空比
- 实际数字信号波形
- 上升时间
:从10%到90% - 下降时间
:从90%到10% - 脉冲宽度
:从50%到50%
- 上升时间
- 波形图和时序图
- 波形图:电路输出值与时间对应的图像
- 时序图:电路状态与时间对应的图像
- 二值数字逻辑和逻辑电平:
1.2 数制
- 十进制:逢十进一,加权展开
- 二进制:
- 逢二进一,加权展开
- 优点:
- 简单可靠
- 运算规则简单
- 波形表示:
- 使用波形来表示数字比较直观
- 最低有效位(LSB):最低位权的那位
- 最高有效位(MSB):最高位权的那位
- 数据传输:
- 由最高位到最低位进行传输
- 并行传输
- 十进制与二进制的转换:
- 二进制转十进制:加权展开法
- 十进制转二进制:
- 整数:倒序除2取余法(除到商为0为止)
- 十进制数较大时,不必逐次除2,可以直接和2的次幂比较
- 小数:乘2顺序取整法(考虑四舍五入,常常多算一位)
- 不一定能完全化为二进制数,在满足误差的情况下四舍五入
- 整数:倒序除2取余法(除到商为0为止)
- 十六进制和八进制:
- 十六进制:逢16进一,其中A~F代表十进制中的10~16
- 因为二进制数很长,所以使用十六进制。
- 同样可以通过加权展开的方式把十六进制的数转化成十进制
- 十六进制和二进制之间的转换:
- 二进制转十六进制:
- 以小数点为界,整数部分从右往左每4位一组,小数部分从左往右每4位一组,不够的补0。
- 每4位二进制数分别转化。
- 十六进制转二进制:
- 每一位数字分别转化:按序排列
- 二进制转十六进制:
- 八进制:逢8进一
- 同样可以加权展开转化成十进制
- 八进制与二进制之间的转化:
- 二进制转八进制:
- 以小数点为界,整数部分从右往左每3位一组,小数部分从左往右每3位一组,不够的补0。
- 每3位二进制数分别转化。
- 八进制转二进制:
- 每一位数字分别转化:按序排列
- 二进制转八进制:
- 十六进制:逢16进一,其中A~F代表十进制中的10~16
1.3 二进制数的算术运算
- 无符号数的算术运算:
加法:
减法:
乘法:
除法:
带符号的二进制的减法运算
二进制的原码、反码和补码:
原码
- 正数的符号位为0
- 负数的符号位为1
- 其余部分用绝对值的二进制形式表示
反码(1‘s complement)
- 正数的反码为其本身
- 负数的反码:
简单方法为:符号位不变,其余部分反转
补码(2‘s complement)
正数的补码与原码相同
负数的补码:
简单方法:在反码的最低位加上1
二进制数减法的补码运算
原理:减去某个数可以通过加上它的负数的补码来完成,并舍弃进位。
注意:
- 参与运算的是补码,运算结果也是补码
- 加数和被加数都采用相同的位数,如果运算结果超过了模,则需将进位丢掉后才能得到正确结果。
- 符号位和数值位一起参与运算,结果的符号位由运算结果决定
溢出:为了进行正确的运算,要求使用正确的位数进行补码运算。
溢出的判别:两个符号相反的数相加不会产生溢出,但是两个符号相同的数相加有可能产生溢出。
判定方式:如果两个加数的符号相同,而和的符号和他们的符号不同,则产生溢出。
1.4 二进制代码
二进制数不仅可以表示数,还可以表示文字(控制符)。
代码:表示文字符号信息的二进制数
编码:按照一定规则编制代码,用以表示十进制数值、字母、符号等过程称为编码
解码:把代码还原成所表示的十进制数、字母、符号的过程称为解码
- BCD码(binary-coded-decimal):二-十进制码,用4位进制数来表示1位十进制中的0~9个十个数码。
常见的BCD码: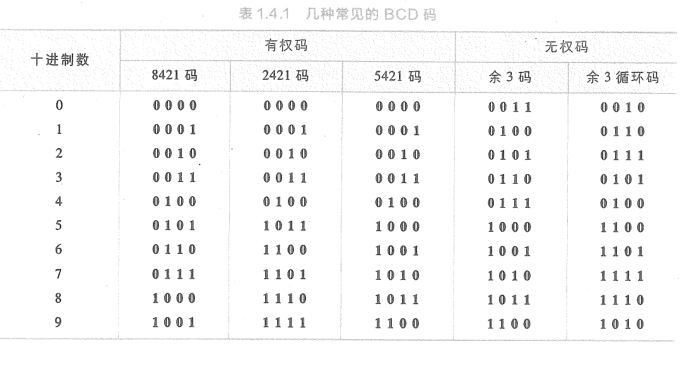
8421码:有权码,位权为8421
2421码:有权码,位权为2421,具有自补性
格雷码: 常见的无权码,具有相邻性、循环性
格雷码的构成方法:
(n+1)位格雷码有
组代码 前
组代码将n位格雷码按照顺序排列,最高位补0 后
组代码将n位格雷码倒序排放,最高位补1 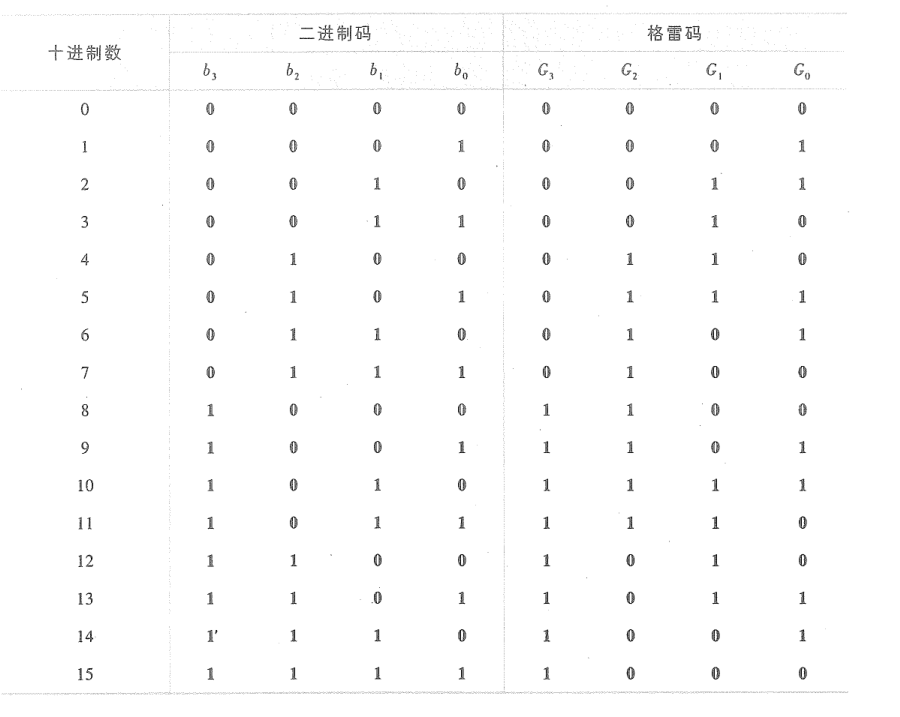
特性:每次格雷码只变换一个数字
除了最高位,各位格雷码存在反射轴,形成镜像
格雷码与二进制码的转化:
- 二进制转格雷码:
- 格雷码最高位和二进制码的最高位相同
- 从左到右,逐渐将二进制码相邻的2位相加(舍去进位)(进行异或运算),作为格雷码的下一位。
- 格雷码转二进制:
- 二进制码的最高位(最左边)与格雷码的最高位相同
- 将产生的每一位二进制码,与下一位(右侧)相邻的格雷码相加(舍去进位)(进行异或运算),作为二进制码的下一位。
- 另一种方法是采用异或表达式
- 格雷码的应用: 错误最小化
- 二进制转格雷码:
ASCII码
- 时间不仅处理数字,而且用于处理字母、符号等文本信息
- 规定了美国信息交换标准代码ASCII(感兴趣可以查阅)
1.5 二值逻辑变量与基本逻辑运算
逻辑运算:按照某种指定的因果关系进行的运算
逻辑运算使用的数学工具是逻辑代数
逻辑代数只有两个可取的值,0和1,因而称为二值逻辑变量
- 与运算:
- 逻辑:只有当一件事的几个条件都具备后,这件事才发生
- 符号:
其中 符号称为与运算符号,在补引起混淆的情况下, 符号可以省略 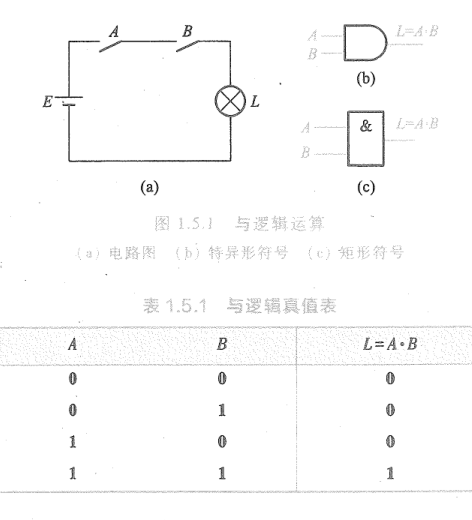
- 或运算:
- 逻辑:当一件事情只要有一个条件得到满足,这件事情就会发生
- 符号:
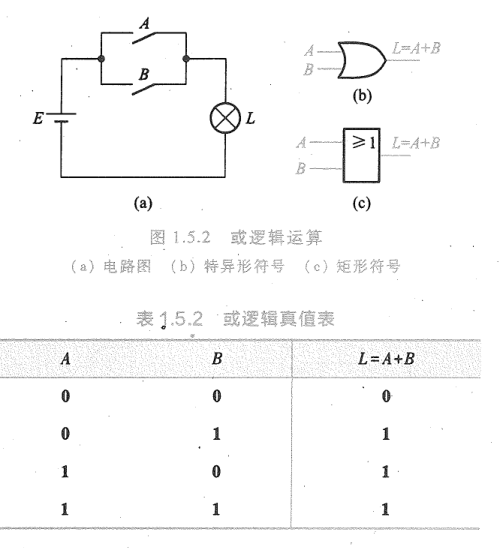
- 非运算:
- 逻辑:一件事情的发生以其相反条件为依据
- 表达:
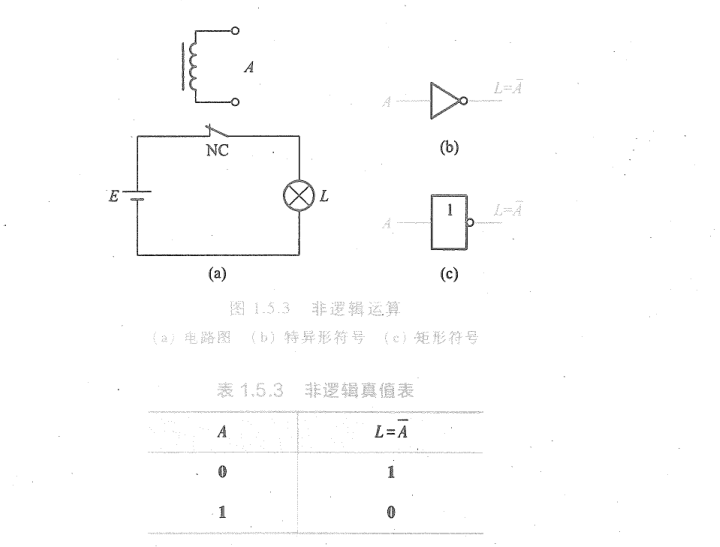
- 常用符合逻辑运算:
- 在实际运算中,更多使用的是它们的组合逻辑运算
- 与非运算:与运算和非运算的结合
- 逻辑表达式:
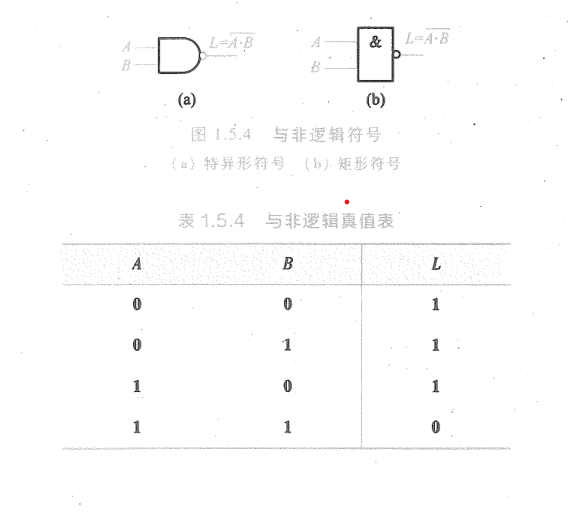
- 逻辑表达式:
- 或非运算:
- 逻辑表达式:
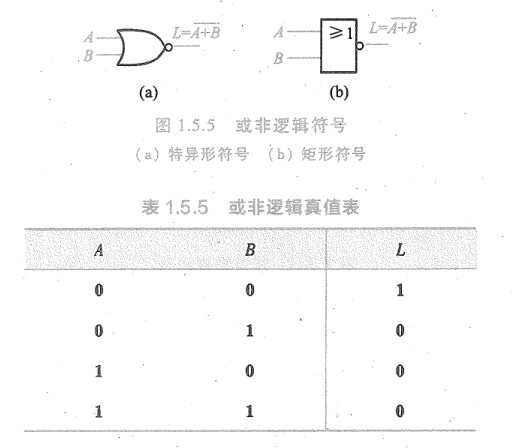
- 逻辑表达式:
- 异或运算:
- 逻辑:两个输入状态相同时,输出为0;两个输入状态不同时,输出为1。
- 逻辑表达式:
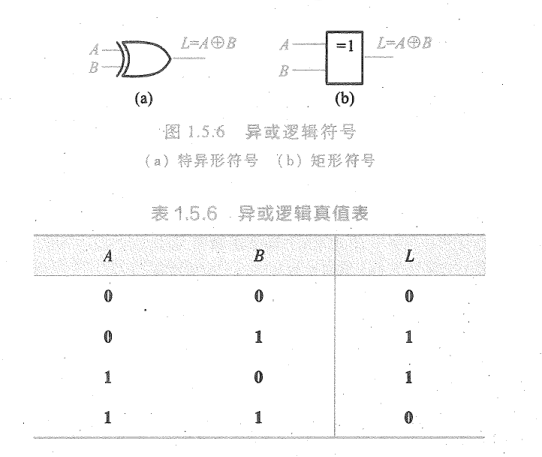
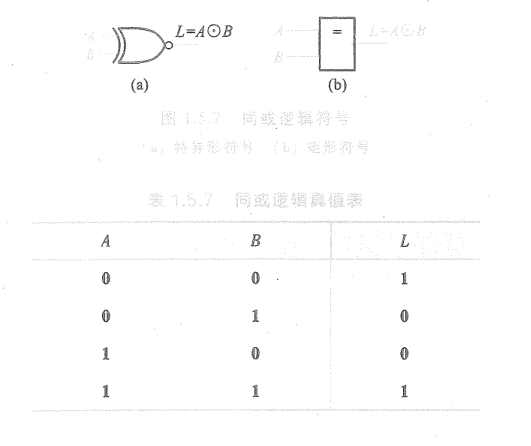
- 同或运算:
- 逻辑:两个输入状态相反时,输出为1,两个输入状态相同时,输出为0。
- 逻辑表达式:
1.6 逻辑函数及其表示方法
逻辑函数:描述输入逻辑变量和输出逻辑变量的因果关系称为逻辑函数。
- 逻辑函数的几种表示方法
- 真值表:将输入变量的所有可能取值与其对应的函数值列出得到表格,称为真值表
- 逻辑函数表达式:如
的表达式 - 逻辑图:用或、与、非等逻辑符号,表示各变量之间的逻辑关系的图形叫做逻辑图
- 波形图:对输入变量随时间的每一种取值,得出相应的输出值,将输入输出按时间顺序排列得到的图形。
- 逻辑函数表示方法之间的转化:
- 真值表转逻辑图:
- 真值表转逻辑表达式
- 利用公式法或者卡诺图化简逻辑表达式
- 根据表达式画出逻辑图
- 逻辑表达式转真值表:
- 从逻辑图的输入端到输出端,逐级写出表达式,知道推导出输出变量
- 化简逻辑表达式
- 把输入变量逐个带入计算,列表得到真值表
- 真值表转逻辑图: